RBM的基本概念
受限玻尔兹曼机(Restricted Boltzmann Machine)由G.Hinton教授提出。RBM是一种无向图模型,也是一种神经网络模型。
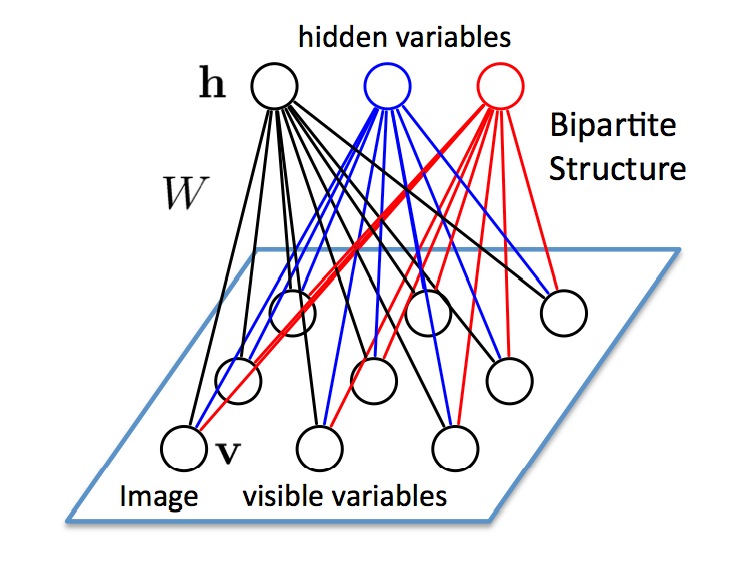
RBM具有两层:可见层(V层),以及隐藏层(H层)
两层神经元之间是全连接的,但是各自层的神经元之间却没有连接,也就是说,RBM的图结构是一种二分图(bipartite graph)。正是这个特点,所以才叫受限玻尔兹曼机。
受限玻尔兹曼机其实允许同一层之间的神经元相连接的。RBM其实是一种简化了的BM模型。
RBM的神经元都是二值化,也就是说只有激活和不激活这两种状态,也就是0或者1。
可见层(V层)和隐藏层(H层)之间的边的权重可以用$W$来表示,$W$是一个$|V|\times|H|$的实数矩阵。 因为$V$和$H$都是二值化的,所以没有连续的可导函数去计算。 Hinton提出了对比散度CD方法,比gibbs方法更快,已经成为求解RBM的标准解法。
RBM的用途
-
对数据进行编码,然后交给监督学习方法进行分类或者回归。可以认为是把它当做一个降维的方法来使用。
-
得到了权重矩阵和偏移量,供BP神经网络初始化训练。如果直接用BP神经网络,初始值选得不好的话,往往会陷入局部极小值。根据实际应用结果表明,直接把RBM训练得到的权重矩阵和偏移量作为BP神经网络初始值,得到的结果会非常地好。这就类似爬山,如果一个风景点里面有很多个山峰,如果让你随便选个山就爬,希望你能爬上最高那个山的山顶,但是你的精力是有限的,只能爬一座山,而你也不知道哪座山最高,这样,你就很容易爬到一座不是最高的山上。但是,如果用直升机把你送到最高的那个山上的靠近山顶处,那你就能很容易地爬上最高的那座山。这个时候,RBM就的角色就是那个直升机。
-
RBM可以估计联合概率p(v,h),如果把v当做训练样本,h当成类别标签(隐藏节点只有一个的情况,能得到一个隐藏节点取值为1的概率),就可以利用利用贝叶斯公式求p(h|v),然后就可以进行分类,类似朴素贝叶斯、LDA、HMM。说得专业点,RBM可以作为一个生成模型(Generative model)使用。
-
RBM可以直接计算条件概率p(h|v),如果把v当做训练样本,h当成类别标签(隐藏节点只有一个的情况,能得到一个隐藏节点取值为1的概率),RBM就可以用来进行分类。说得专业点,RBM可以作为一个判别模型(Discriminative model)使用。