原文链接：Softmax 函数的特点和作用是什么？ - 忆臻的回答 - 知乎
softmax函数
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类。
假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是：
\[S_i= \frac{ {e}^{V_i}}{\sum_{j}^{}{ {e}^{V_j}}}\]更加形象的图如下：
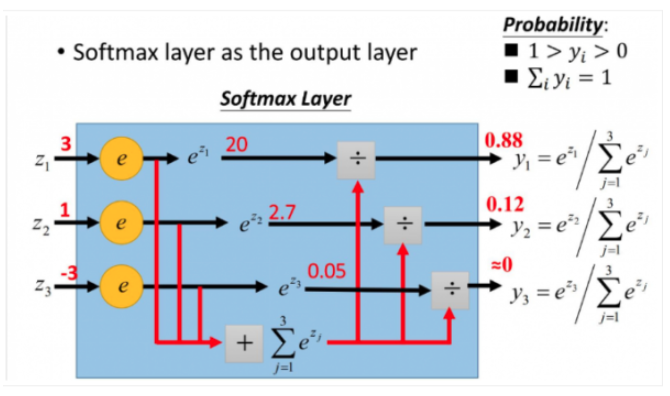
softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！
softmax相关求导
下面我们举出一个简单例子
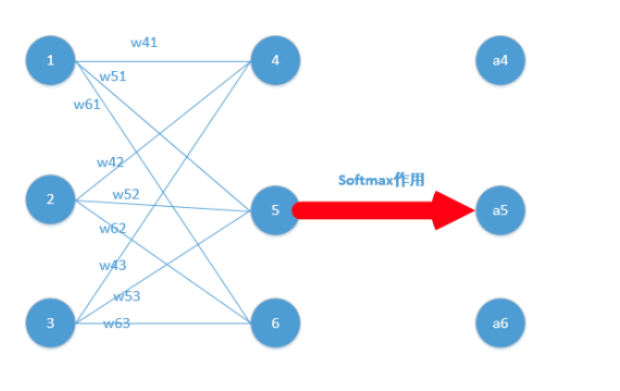我们能得到下面公式：
z4,z5,z6分别代表结点4,5,6的输出，01,02,03代表是结点1,2,3往后传的输入.
那么我们可以经过softmax函数得到:
\[a_4 = \frac{ {e}^{z_4}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}} \\ a_5 = \frac{ {e}^{z_5}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}} \\ a_6 = \frac{ {e}^{z_6}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}}\]接下来，利用梯度下降方法更新梯度。要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数，为什么使用交叉熵损失函数，不是这篇文章重点，后面有时间会单独写一下为什么要用到交叉熵函数（这里我们默认选取它作为损失函数）
交叉熵函数形式如下：
\[Loss = - \sum_{i}y_i ln_{a_i}\]其中y代表我们的真实值，a代表我们softmax求出的值。i代表的是输出结点的标号！在上面例子，i就可以取值为4,5,6三个结点（当然我这里只是为了简单，真实应用中可能有很多结点）
但是实际上不是这样的，我们往往在真实中，如果只预测一个结果，那么在目标中只有一个结点的值为1，比如我认为在该状态下，我想要输出的是第四个动作（第四个结点）,那么训练数据的输出就是a4 = 1,a5=0,a6=0，哎呀，这太好了，除了一个为1，其它都是0，那么所谓的求和符合，就是一个幌子，我可以去掉啦！
为了形式化说明，我这里认为训练数据的真实输出为第j个为1，其它均为0！
那么Loss就变成了,累和已经去掉了，太好了。现在我们要开始求导数了！
我们在整理一下上面公式，为了更加明白的看出相关变量的关系：
其中$y_i=1$，$Loss=-lna_j$
那么形式越来越简单了，求导分析如下：
参数的形式在该例子中，总共分为w41,w42,w43,w51,w52,w53,w61,w62,w63.这些，那么比如我要求出w41,w42,w43的偏导，就需要将Loss函数求偏导传到结点4，然后再利用链式法则继续求导即可，举个例子此时求w41的偏导为:
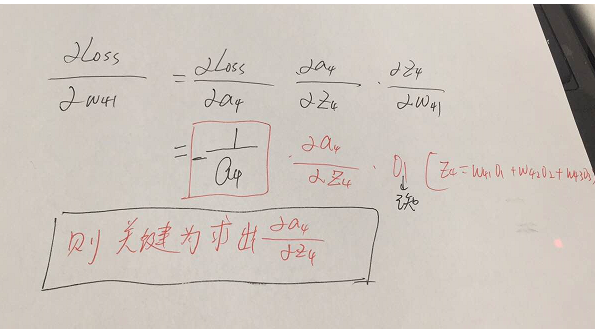
w51…..w63等参数的偏导同理可以求出，那么我们的关键就在于Loss函数对于结点4,5,6的偏导怎么求，如下：
这里分为俩种情况：
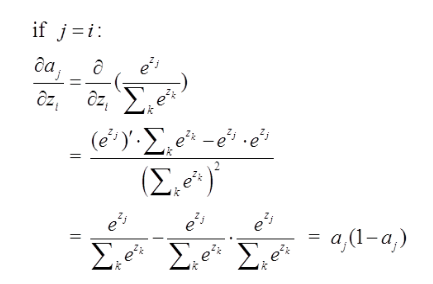
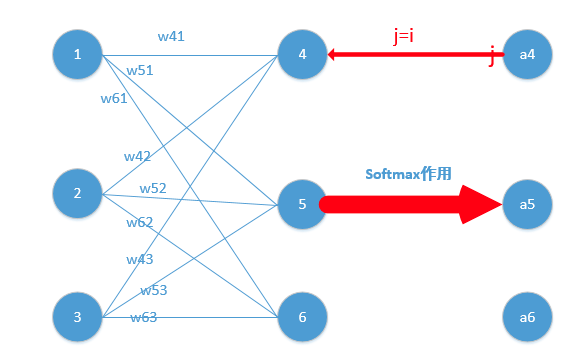
j=i对应例子里就是如下图所示：
比如我选定了j为4，那么就是说我现在求导传到4结点这！
那么由上面求导结果再乘以交叉熵损失函数求导
$Loss=-lna_j，$他的导数是$-\frac{1}{a_j}$，与上面$a_j(1-a_j)$相乘为$a_j-1$。形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可，后面还会举例子！）那么我们可以得到Loss对于4结点的偏导就求出了了（这里假定4是我们的预计输出）
第二种情况为：
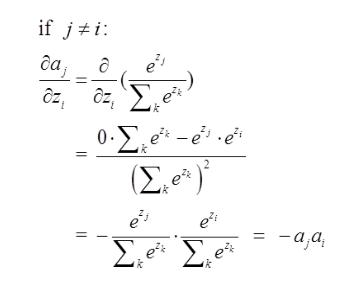
这里对应我的例子图如下，我这时对的是j不等于i，往前传：
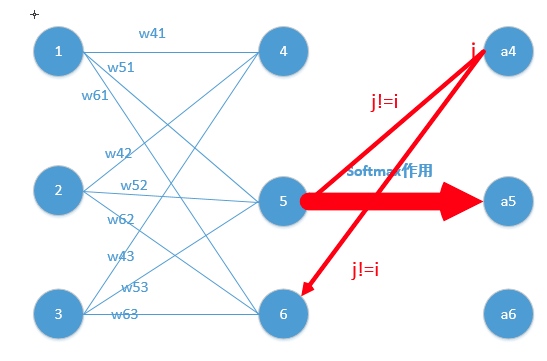
那么由上面求导结果再乘以交叉熵损失函数求导
$Loss=-lna_j$，他的导数是$-\frac{1}{a_j}$，与上面$-a_ja_i$相乘为$a_i$。（形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可，后续例子会讲到）这里就求出了除4之外的其它所有结点的偏导，然后利用链式法则继续传递过去即可！我们的问题也就解决了！
举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],那么经过softmax函数作用后概率分别就是：
\[\begin{bmatrix} \frac{ {e}^{z_4}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}} & \frac{ {e}^{z_5}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}} & \frac{ {e}^{z_6}}{ {e}^{z_4}+{e}^{z_5}+{e}^{z_6}} \end{bmatrix}\] \[\begin{bmatrix} 0.0903 & 0.2447 & 0.665 \end{bmatrix}\]如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是
\[\begin{bmatrix} 0.0903 & 0.2447-1 & 0.665 \end{bmatrix}\]是不是非常简单！！然后再根据这个进行back propagation就可以了